3. 参数学习
3.1 梯度下降 Gradient Descent
现在,我们有了假设函数,并且有了一种方法来衡量它与数据的拟合程度。 现在需要做的是估计假设函数中的参数。 在此引入梯度下降。

当代价函数位于图中凹坑的最底部时,即当其值最小,我们就成功了。红色箭头显示图中的最小点。
方法是计算代价函数的导数(函数的切线)。切线的斜率是该点的导数,它提供一个方向。我们沿下降最陡的方向逐步降低代价函数。每个步骤的大小由参数α(称为学习率)确定。
例如,上图中每个 “X” 之间的距离代表由参数α确定的步长。较小的α将导致较小的步长,较大的α将导致较大的步长。前进的方向由J(θ0,θ1)的偏导确定。根据在图上的起点不同,可能会在不同的点结束。上图为我们提供了两个不同的起点,它们以两个不同的位置结束。
梯度下降算法为:

其中j = 0,1代表特征索引。
在每次迭代j时,应同时更新参数θ1,θ2,…,θn。在第j次迭代中计算另一个参数之前,更新特定参数会导致错误。

3.2 梯度下降I Gradient Descent I
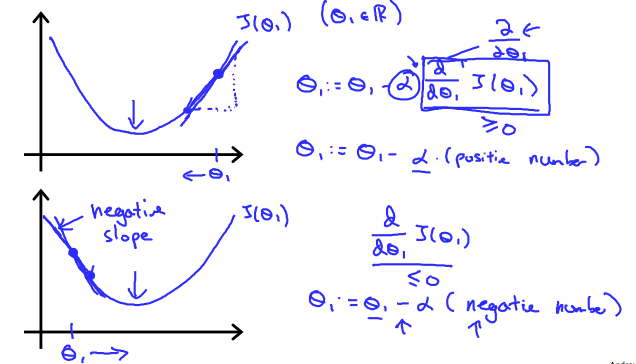
单个参数公式为:

下图显示,当斜率为负时,θ1的值增大,当斜率为正时,θ1的值减小:
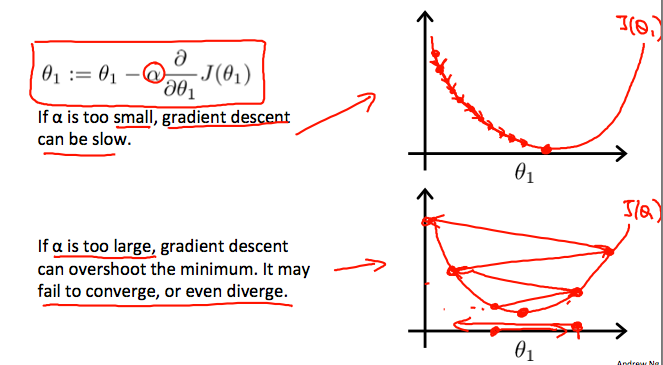
当学习率α太大或太小:
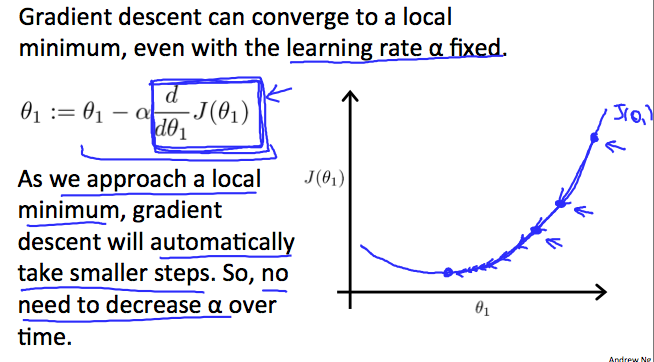
梯度下降如何以固定步长α收敛?
当我们接近凸函数的底部时,J(θ1)的偏导接近0。因此我们得到:
当专门用于线性回归时,可以得出新的形式的梯度下降方程。 我们可以用实际成本函数和实际假设函数代替,并将等式修改为:

其中m是训练集θ0的大小,该常数将与θ1同时变化,xi,yi是给定训练集(数据)的值。
以下是单个示例的偏导:

所有这些的要点是,从对假设开始,重复应用这些梯度下降方程,则假设将变得越来越准确。
因此,这只是原始成本函数J的梯度下降。此方法用于每训练集中的每个示例,称为批梯度下降。 请注意,虽然梯度下降通常可能会受到局部极小值的影响,但是我们在此处为线性回归提出的优化问题只有一个全局最优,而没有其他局部最优。 因此,梯度下降总是会收敛(假设学习率α不太大)到全局最小值。 J是一个凸二次函数。
