数据结构之栈
栈的概念
线性表,运算受限(仅允许一端的插入和删除)
棒球比赛
你现在是棒球比赛记录员。
给定一个字符串列表,每个字符串可以是以下四种类型之一:
1.整数(一轮的得分):直接表示您在本轮中获得的积分数。
2.“+”(一轮的得分):表示本轮获得的得分是前两轮有效 回合得分的总和。
3.“D”(一轮的得分):表示本轮获得的得分是前一轮有效 回合得分的两倍。
4.“C”(一个操作,这不是一个回合的分数):表示您获得的最后一个有效 回合的分数是无效的,应该被移除。
每一轮的操作都是永久性的,可能会对前一轮和后一轮产生影响。
你需要返回你在所有回合中得分的总和。
示例 1:
输入: [“5”,“2”,“C”,“D”,“+”]
输出: 30
解释:
第1轮:你可以得到5分。总和是:5。
第2轮:你可以得到2分。总和是:7。
操作1:第2轮的数据无效。总和是:5。
第3轮:你可以得到10分(第2轮的数据已被删除)。总数是:15。
第4轮:你可以得到5 + 10 = 15分。总数是:30。
示例 2:
输入: [“5”,“-2”,“4”,“C”,“D”,“9”,“+”,“+”]
输出: 27
解释:
第1轮:你可以得到5分。总和是:5。
第2轮:你可以得到-2分。总数是:3。
第3轮:你可以得到4分。总和是:7。
操作1:第3轮的数据无效。总数是:3。
第4轮:你可以得到-4分(第三轮的数据已被删除)。总和是:-1。
第5轮:你可以得到9分。总数是:8。
第6轮:你可以得到-4 + 9 = 5分。总数是13。
第7轮:你可以得到9 + 5 = 14分。总数是27。
注意:
输入列表的大小将介于1和1000之间。
列表中的每个整数都将介于-30000和30000之间。
export default (arr)=>{
// 用数组来实现堆栈结构,pop,push(从后面添加,从后面删除)
let result=[]
// 上一轮的数据
let pre1
// 上上轮的数据
let pre2
// 对数组进行遍历,遍历的目的是处理得分
arr,forEach(item=>{
switch(item){
case 'C':
if(result.length){
result.pop()
}
break
case 'D':
pre1=result.pop()
result.push(pre1,pre1*2)
break
case '+':
pre1=result.pop()
pre2=result.pop()
result.push(pre2,pre1,pre1+pre2)
break
default:
result.push(item*1)
break
}
})
return result.reduce((total,num)=>{total+num})
}
最大矩形
给定一个仅包含 0 和 1 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。
示例:
输入:
[
[“1”,“0”,“1”,“0”,“0”],
[“1”,“0”,“1”,“1”,“1”],
[“1”,“1”,“1”,“1”,“1”],
[“1”,“0”,“0”,“1”,“0”]
]
输出: 6
export default (arr) => {
let result = []
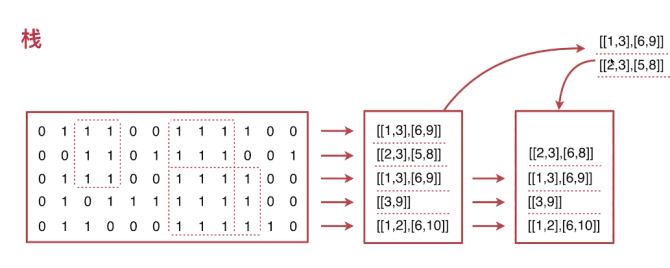
let reg = /1{2,}/g
// 把二位数组重新表达,把相邻的1提取出来(起始点+截止点)
arr = arr.map(item => {
let str = item.join('')
let r = reg.exec(str)
let rs = []
while (r) {
rs.push([r.index, r.index + r[0].length - 1])
r = reg.exec(str)
}
return rs
})
// 通过递归计算相邻的矩阵
let maxRect = (arr, result, n = 1) => {
// 弹出第一行
let top = arr.pop()
// 弹出第二行
let next = arr.pop()
// 记录第一行的每一个起始点和截止点
let tt
// 记录第二行的每一个起始点和截止点
let nn
// 记录交叉的起始索引
let start
// 记录交叉的截止索引
let end
let width = 1
let maxWidth = 1
n++
for (let i = 0, il = top.length; i < il; i++) {
tt = top[i]
for (let j = 0, jl = next.length; j < jl; j++) {
nn = next[j]
width = Math.min(tt[1], nn[1]) - Math.max(tt[0], nn[0])
// 修改避免相邻两个数的差值为1(实际宽度为2)没有为start,end赋值导致的bug,应该加上=
if (width >= maxWidth) {
maxWidth = width
start = Math.max(tt[0], nn[0])
end = Math.min(tt[1], nn[1])
}
}
}
// 如果没有找到交叉点
if (start === undefined || end === undefined) {
if (n < 3) {
return false
} else {
width = top[0][1] - top[0][0] + 1
if (width > 1) {
result.push((n - 1) * width)
}
}
} else {
// 找到交叉点继续下一行
if (arr.length > 0) {
arr.push([
[start, end]
])
maxRect(arr, result, n++)
} else {
// 从某一行一直计算到最后一行,这个时候start和end一直有值,所以不会进入到if层,这个时候n就是累计的行数(高),end-start+1就是宽
result.push(n * (end - start + 1))
}
}
}
while (arr.length > 1) {
maxRect([].concat(arr), result)
arr.pop()
}
// 取最大值
let max = 0
let item = result.pop()
while (item) {
if (item > max) {
max = item
}
item = result.pop()
}
return max > 0 ? max : -1
}
export default (arr) => {
let result = []
let reg = /1{2,}/g
// 把二位数组重新表达,把相邻的1提取出来(起始点+截止点)
arr = arr.map(item => {
let str = item.join('')
let r = reg.exec(str)
let rs = []
while (r) {
rs.push([r.index, r.index + r[0].length - 1])
r = reg.exec(str)
}
return rs
})
// [ [], [ [ 2, 4 ] ], [ [ 0, 4 ] ], [] ]
// 通过递归计算相邻的矩阵
let maxRect = (arr, result, n = 1) => {
// 弹出第一行
let top = arr.pop()
// 弹出第二行
let next = arr.pop()
// 记录第一行的每一个起始点和截止点
let tt
// 记录第二行的每一个起始点和截止点
let nn
// 记录交叉的起始索引
let start
// 记录交叉的截止索引
let end
let width = 1
let maxWidth = 1
n++
for (let i = 0, il = top.length; i < il; i++) {
tt = top[i]
for (let j = 0, jl = next.length; j < jl; j++) {
nn = next[j]
width = Math.min(tt[1], nn[1]) - Math.max(tt[0], nn[0])
// 修改避免相邻两个数的差值为1(实际宽度为2)没有为start,end赋值导致的bug,应该加上=
if (width >= maxWidth) {
maxWidth = width
start = Math.max(tt[0], nn[0])
end = Math.min(tt[1], nn[1])
}
}
}
// 如果没有找到交叉点
if (start === undefined || end === undefined) {
if (n < 3) {
return false
} else {
width = top[0][1] - top[0][0] + 1
if (width > 1) {
result.push((n - 1) * width)
}
}
} else {
// 找到交叉点继续下一行
if (arr.length > 0) {
arr.push([
[start, end]
])
maxRect(arr, result, n++)
} else {
// 从某一行一直计算到最后一行,这个时候start和end一直有值,所以不会进入到if层,这个时候n就是累计的行数(高),end-start+1就是宽
result.push(n * (end - start + 1))
}
}
}
while (arr.length > 1) {
maxRect([].concat(arr), result)
arr.pop()
}
// 取最大值
let max = 0
let item = result.pop()
while (item) {
if (item > max) {
max = item
}
item = result.pop()
}
return max > 0 ? max : -1
}

