写在前面
在Coursera的机器学习中配套有相关的练习,然而这些练习是使用Octave实现的。不过,作为一个Python的初学者当然得知道强大的Python也是可以实现这些练习的,接下来就对其中的一些练习的关键代码进行分享。
线性回归的实现
文件读取
作业中提供的csv文件含有两列数据。
x是Profit in $10,000s, y代表了Population of City in 10,000s。
所以我们先需要读取这个csv文件,使用csv中的reader方法便可以轻松实现。
with open(filename, 'r') as f:
reader = csv.reader(f)
读取文件之后先别急,我们可以使用matplotlib中的方法将数据plot出来看看它的分布情况。
plt.plot(data_x, data_y, 'rx', 10)
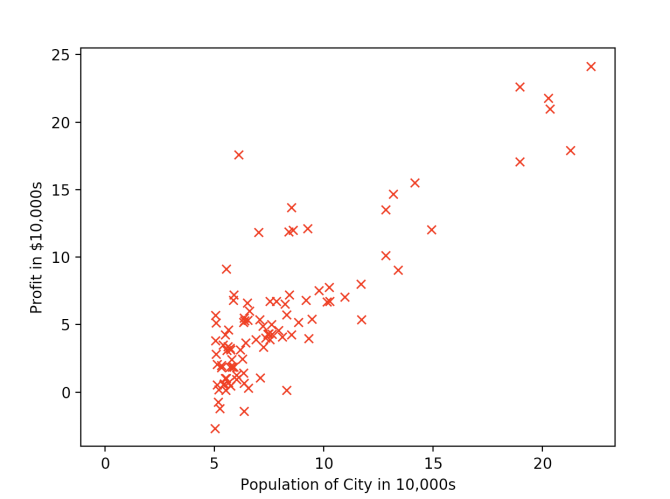
转成矩阵
当然在学习过程中,需要将数据都处理成矩阵,提高运算效率。之前也分享过简单的矩阵知识。而在Python中可以使用numpy中的方法实现这个操作。
data_x = [[1, row] for row in data_x]
matrix_x = np.mat(data_x)
可能有人会好奇为什么要在数据前面多加一列1呢,问出这个问题的同学请好好反省,可别忘了其中还有个theta0存在。
损失函数
还记得我们有一个关键的函数叫损失函数吗,如果不记得那就看看下图回顾一下。
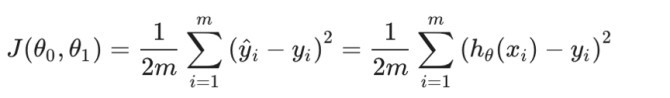
只需要用代码将图中的损失函数表达出来就行了。嘛,其实就是求个方差。这时就不难发现将数据处理成矩阵的好处了。
# compute suqare errors
sqrErrors = np.power((data_x * theta_in - data_y), 2).sum()
# compute cost
J = sqrErrors / (2 * len(data_y))
梯度下降
那么有了损失函数之后需要什么呢,当然是一个优化函数,这时候我们就需要使用梯度下降法对其进行优化了,如果对梯度下降没有印象了,就看看下图。

与上面的相同,只需要把它写出来就行。值得注意的是我们需要初始化一个cost,用来存放不断迭代更新的损失。但是一定要清楚我们求的东西到底是什么,我们求的东西是让损失最小的theta。
J_history = np.zeros([nums_ite, 1])
for ite in range(1, nums_ite):
theta = theta - select_alpha / m * data_x.T * (data_x * theta - data_y)
J_history[ite] = compute_cost(data_x, data_y, theta)
此处我们就基本把线性回归的代码实现了,这就是一个十分简单的实现。
结果展示
我们把Contour图画出来,可以看到损失一步一步向内下降,我们也可以看到红色的x。这个点就代表了当损失最小。
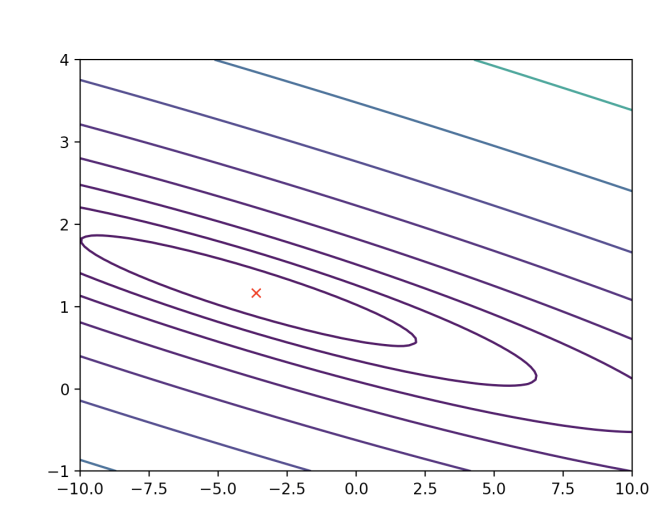
写在后面
这就是一个比较简单的线性回归代码实现了,当然这些代码只是一些关键性代码,如果要自己实现还需要进行一定的补充。一些画图的方法也都可以百度到,不妨尝试一下。
