2. 模型与代价函数
2.1 模型展示
x(i) 表示输入变量 (在本示例中为居住区域)
y(i) 表示预测的输出或目标变量 (在本示例中为价格)
(x(i), y(i) ) 被称为训练示例
x(i) (i = 1, . . . , m )被称为训练集。 注意,符号中的上标(i)只是训练集中的一个索引,与幂运算无关。
使用X表示输入值的空间,并使用Y表示输出值的空间。 在此示例中,X = Y = ℝ
当要预测的目标变量是连续的时(例如在住房示例中)为回归问题。
当y只能采用少量离散值时(例如,假设给定居住面积,我们想预测某个住宅是房子还是公寓),称其为分类问题。
2.2 代价函数
可以用来衡量假设函数的准确性。 是定义在整个训练集上的,是所有样本误差的平均,计算预测值和实际输出y的平方差的均值。
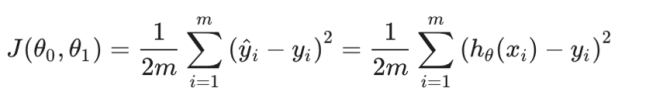
该函数称为“平方差函数”或“均方差”。 设置1/2以方便计算梯度下降,因为平方函数的导数项将抵消1/2项。
我们需要找到能拟合下图的线:
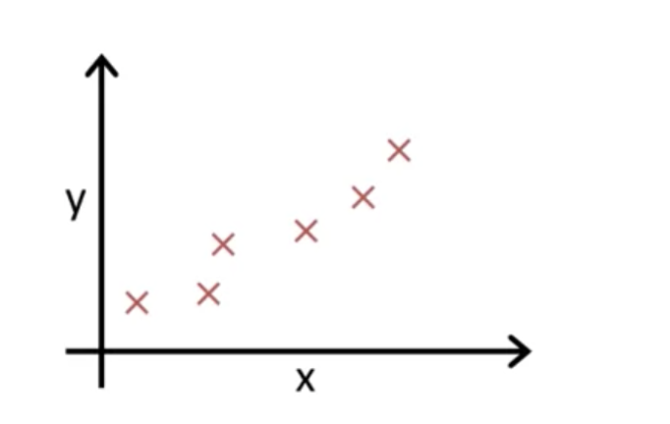
结果如下:

2.3 把它画出来
训练数据集会散布在x-y平面上。 绘制一条直线(由hθ(x)定义)穿过这些分散的数据点。
目标是获得最适合的线。 最佳可能的线应是这样,以使散射点与该线的平均垂直垂直距离最小。
理想情况下,直线应穿过训练数据集中的所有点。 在这种情况下,J(θ0,θ1)的值为0。
以下示例显示了成本函数为0的理想情况:
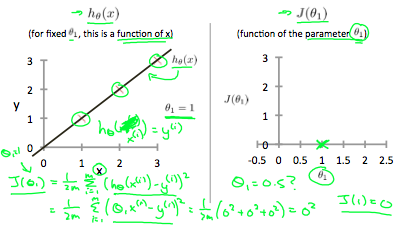
当θ1= 0.5时,可以看到从拟合到数据点的垂直距离增加:
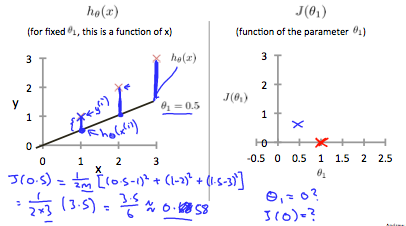
绘制其他几个点可得出下图:


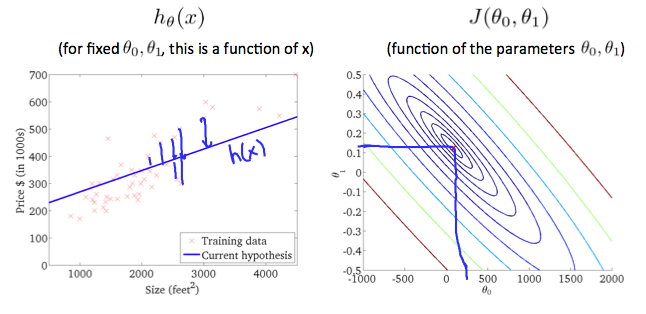
2.3.1 等高线图
示例:

选择任何颜色并沿“圆”移动,得到的值是相同的。 例如,在上面的绿线上找到的三个绿点的J(θ0,θ1)值相同。带圆圈的x在左侧显示当θ0 = 800且θ1= -0.15时的值。
取另一个h(x) 并绘制其等高线图,将得到以下图形:
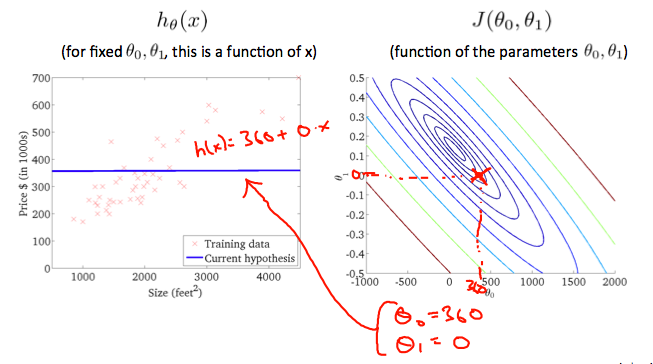
当θ0 = 360且θ1 = 0时,等高线图中的 J(θ0, θ1) 值更靠近中心,从而降低了成本函数误差。现在给假设函数一个稍微为正的斜率,可以更好地拟合数据。