计算相似度 - sdk社区

在机器学习中，经常要度量两个对象的相似度，例如k-最近邻算法，即通过度量数据的相似度而进行分类。在无监督学习中，K-Means算法是一种聚类算法，它通过欧几里得距离计算指定的数据点与聚类中心的距离。在推荐系统中，也会用到相似度的计算（当然还有其他方面的度量）。

本文中，将介绍业务实践中最常用的几种相似度的度量方法。

基于相似性的度量

皮尔逊相关系数
斯皮尔曼秩相关系数
肯德尔秩相关系数
余弦相似度
雅卡尔相似度

基于距离的度量

欧几里得距离
曼哈顿距离

1. 基于相似性的度量

1.1 皮尔逊相关系数

皮尔逊相关系数度量两个随机变量之间的线性关系，包括相关程度和方向。这两个随机变量可以是连续型，也可以是离散型。

计算公式如下：

$\frac{\sum_{i=1}^n(x_i-\overline x)(y_i - \overline y)}{\sqrt{\sum_{i=1}^n(x_i-\overline x)^2}\sqrt{\sum_{i=1}^n(y_i-\overline y)^2}} </annotation></semantics></math>$

其中，\overline x = \frac{1}{n}\sum_{i=1}^nx_i, \overline y = \frac{1}{n}y_i 。
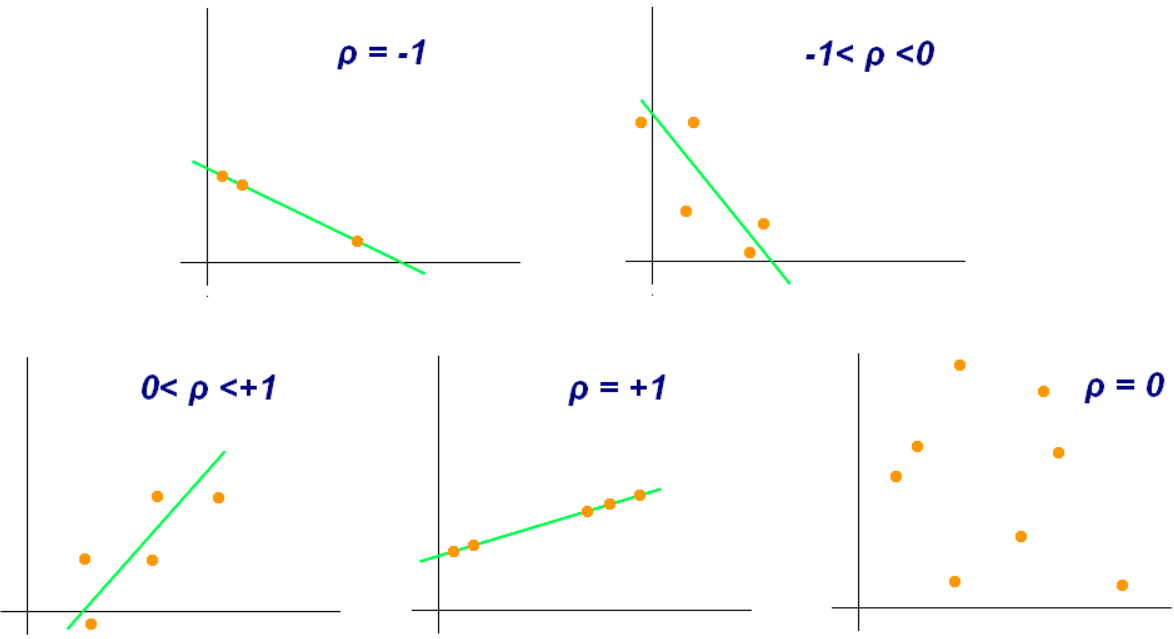
皮尔逊相关系数的范围在 $ [-1,1] $， -1意味着两者负相关，1代表正相关。

用python实现皮尔逊相关系数的计算：

import numpy as np
from scipy.stats import pearsonr
import matplotlib.pyplot as plt。

# 设置随机数的种子
np.random.seed(42)
# 创建随机数
x = np.random.randn(15)
y = x + np.random.randn(15)

# 作图
plt.scatter(x, y)
plt.plot(np.unique(x), np.poly1d(np.polyfit(x, y, 1))(np.unique(x)))
plt.xlabel('x')
plt.ylabel('y')
plt.show()

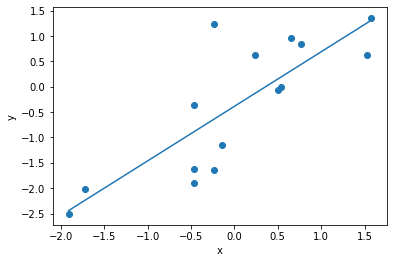
# 计算皮尔逊相关系数
corr, _ = pearsonr(x, y)
print('Pearsons correlation: %.3f' % corr)

输出：Pearsons correlation: 0.810

1.2 斯皮尔曼秩相关系数

斯皮尔曼秩相关系数（Spearman’s correlation）常用于非参数统计。所谓非参数统计，即概率分布不依靠参数（常见的正态分布、二项分布等都是参数统计）。最常见的非参数统计，是统计数据的秩，而不是原始的值。斯皮尔曼秩相关系数的计算方法，与皮尔逊相关系数类似，区别就在于斯皮尔曼相关系数中使用的是数据的秩。

为了计算斯皮尔曼相关系数，我们首先需要将每个原始数据转化为等级数据，建立如下映射关系：

$\to X^r</annotation></semantics></math>$ ， $encoding="application/x-tex">x_i \to x_i^r</annotation></semantics></math>$
$\to Y^r</annotation></semantics></math>$ ， $encoding="application/x-tex">x_i \to y_i^r</annotation></semantics></math>$

例如，原始数据为 [0, -5, 4, 7]，则对应的等级数据为[2, 1, 3, 4]。

用以下方法计算斯皮尔曼相关系数:

$\frac{\sum_{i=1}^n(x^r_i - \overline x^r)(y^r_i - \overline y^r)}{\sqrt{\sum_{i=1}^n(x^r_i - \overline x^r)^2}\sqrt{\sum_{i=1}^n(y^r_i - \overline y^r)}}</annotation></semantics></math>$

其中 $encoding="application/x-tex">\overline x^r = \frac{1}{n}\sum_{i=1}^nx^r_i, \overline y^r = \frac{1}{n}\sum_{i=1}^n y^r_i</annotation></semantics></math>$ 。

斯皮尔曼秩相关系数可以度量两个量之间的非线性相似度，这是和皮尔逊相关系数的重要区别。它的取值范围从-1到+1。

下面的图显示了了皮尔逊相关系数和斯皮尔曼相关系数之间的差异。

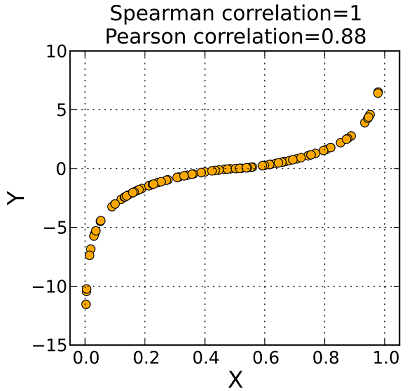
图中的数据是呈非线性单调，如果用皮尔逊相关系数——它度量线性关系，得到的相关系数是 0.88 ，而斯皮尔曼秩相关系数是 1 。

在研究数据的相似度时，根据经验，建议分别计算皮尔逊相关系数和斯皮尔曼秩相关系数。

在Python中，实现斯皮尔曼秩相关系数的方法如下：

from scipy.stats import spearmanr
# 计算斯皮尔曼秩相关系数
corr, _ = spearmanr(x, y)
print(‘Spearmans correlation: %.3f’ % corr)

输出结果：Spearmans correlation: 0.836

1.3 肯德尔秩相关系数

肯德尔秩相关系数与斯皮尔曼相关系数类似，都是非参数统计中度量相似度的方法，都依据原始数据的等级数据进行计算，不是原始数据。

肯德尔秩相关系数的值也是在 -1 和 +1 之间，其中 -1 表示两个变量之间的强负相关，1 表示两个变量之间的强正相关。

相对于斯皮尔曼秩相关系数，肯德尔秩相关系数具有统计学上的优势，如果样本量比较大了，对肯德尔秩相关系数的影响较小，特别是手工计算时，体现出了优势。但是，如果用程序实现计算，从算法的角度看，斯皮尔曼秩相关系数的时间复杂度是 $O (n l o g (n))$ ，肯德尔秩相关系数的时间复杂度是 $encoding="application/x-tex">O(n^2)</annotation></semantics></math>$ ，即斯皮尔曼秩相关系数在计算速度上有优势。

计算肯德尔秩相关系数的第一步与前述斯皮尔曼秩相关系数一样，也是要得到原始数据的等级数据，然后依据下面的公式计算：

$\frac{2}{n(n-1)}\sum_{i\lt j}sgn(x_i^r - x_j^r)sgn(y_i^r - y_i^r)</annotation></semantics></math>$

其中

$encoding="application/x-tex">sgn(x_i^r-x_j^r)=\begin{cases}-1,\quad &(x_i^r \lt x_j^r) \\ 0, &(x_i^r = x_j^r) \\ 1 &(x_i^r \gt x_j^r)\end{cases},(i \lt j)</annotation></semantics></math>$

在Python中实现肯德尔相关系数的计算，方法如下：

from scipy.stats import kendalltau
corr, _ = kendalltau(x, y)
print(‘Kendalls tau: %.3f’ % corr)

输出结果：Kendalls tau: 0.695

1.4 余弦相似度

余弦相似度计算两个向量或者随机变量之间夹角的余弦，公式如下：

S(X,Y) = \frac{\pmb{x}\cdot\pmb{y}}{\begin{Vmatrix}\pmb{x}\end{Vmatrix}\begin{Vmatrix}\pmb{y}\end{Vmatrix}}=\frac{\sum_{i=1}^nx_iy_i}{\sqrt{\sum_{i=1}^nx_i^2}\sqrt{\sum_{i=1}^ny_i^2}}

下图显示了余弦函数的特点，从中可知，余弦函数的取值在 -1 到 +1 之间。如果向量指向相同的方向，余弦相似度是+1。如果向量指向相反的方向，余弦相似度为-1。

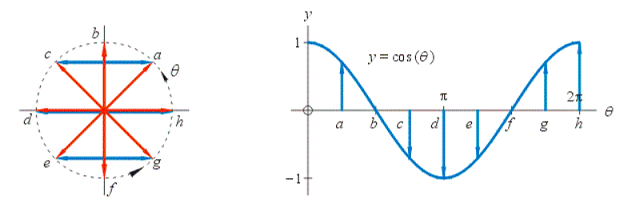
余弦相似度在文本分析中很常见。它用于确定文档之间的相似程度，而不考虑文档的大小。

下面的程序中演示了在Python语言中实现余弦相似度的方法。

from sklearn.metrics.pairwise import cosine_similarity
cos_sim = cosine_similarity(x.reshape(1,1),y.reshape(1,-1))
print('Cosine similarity: %.3f' % cos_sim)

输出结果：Cosine similarity: 0.773

1.5 雅卡尔相似度

雅卡尔相似度（Jaccard similarity），又称为“雅卡尔指数”（Jaccard index）、“并交比”（Intersection over Union），是用于比较两个集合相似性的统计量。设 A、B 为两个有限样本集合，雅卡尔相似度定义为：

$\frac{|A\cap{B}|}{|A\cup{B}|}=\frac{|A \cap{B}|}{|A| + |B| - |A \cap{B}|} </annotation></semantics></math>$

下图以可视化方式解释了定义式的含义。

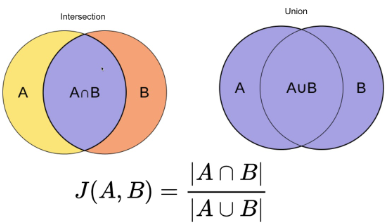
我们可以看到，雅卡尔相似度是交集的大小除以样本集的并集的大小。

余弦相似度和雅卡尔相似度都是度量文本相似度的常用方法，但雅卡尔相似度在计算上成本较高，因为它要将一个文档的所有词汇匹配到另一个文档。实践证明，雅卡尔相似度在检测重复项方面很有用——集合运算的特点。

用Python实现雅卡尔相似度的计算过程：

from sklearn.metrics import jaccard_score
A = [1, 1, 1, 0]
B = [1, 1, 0, 1]
jacc = jaccard_score(A,B)
print(‘Jaccard similarity: %.3f’ % jacc)

输出：Jaccard similarity: 0.500

2. 基于距离的度量

2.1 欧几里得距离

欧几里德距离是两个向量之间的直线距离。

设两个向量 \pmb{x} 和 \pmb{y} ，可以进行如下计算：

d(\pmb{x}, \pmb{y})=\begin{Vmatrix}\pmb{x}-\pmb{y}\end{Vmatrix}=\sqrt{\sum_{i=1}^n(x_i-y_i)^2}

与前述的余弦相似度和雅卡尔相似度相比，欧几里得距离很少用于NLP中，它更适用于计算连续型变量间的距离。要注意，欧几里得距离与度量单位有关，所以，在计算的时候，首先要进行单位统一。

在Python中计算欧几里得距离的基本方法是：

from scipy.spatial import distance
dst = distance.euclidean(x,y)
print(‘Euclidean distance: %.3f’ % dst)

输出结果：Euclidean distance: 3.273

2.2 曼哈顿距离

曼哈顿距离，也叫做城市街区距离，与欧几里得距离不同，它是从一个向量到另一个向量的距离。可以想象，当你不能穿过建筑物时，这个度量可以用来计算两点之间的距离。

计算曼哈顿距离的公式如下:

$\sum_{i=1}^n|x_i-y_i|</annotation></semantics></math>$

下图中的绿线表示欧几里德距离，而紫线表示曼哈顿距离。

在许多机器学习应用中，欧几里德距离是首选的度量标准。然而，对于高维数据来说，曼哈顿距离更可取，因为它产生了更有说服力的结果。

在Python中实现曼哈顿距离的方法是：

from scipy.spatial import distance
dst = distance.cityblock(x,y)
print(‘Manhattan distance: %.3f’ % dst)

输出结果：Manhattan distance: 10.468

总结

本文概述了在实践中度量相似度的常见方法。在实际的问题中，没有简单的“如果. … 那么 … ”流程图来选择使用哪一种相似性度量方法。我们首先需要了解和研究数据。然后，要想为给定的数据科学问题找到量化相似性的正确方法，始终需要针对每一个具体案例做出具体决策。

注：本文内容是以2021年5月份即将出版的《机器学习数学基础》（作者：齐伟）中的某章节内容为基础编写而成。更详细的相关内容，请参阅此书。

参考资料

齐伟.机器学习数学基础.北京:电子工业出版社（预计2021年5月份出版）
齐伟.数据准备和特征工程.北京:电子工业出版社.2020
https://towardsdatascience.com/calculate-similarity-the-most-relevant-metrics-in-a-nutshell-9a43564f533e