JS基础算法(数据结构之二叉树篇)

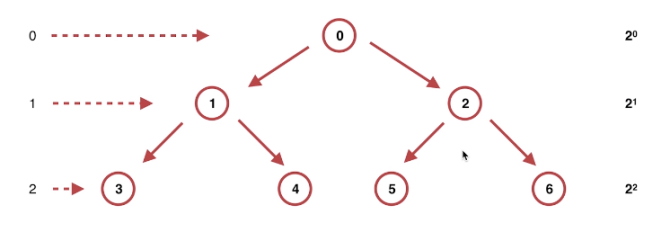
特性

一个节点只有两个子节点，左节点和右节点

实现二叉树结构

// 二叉树的节点
class Node {
    constructor(val) {
        this.val = val
        this.left = this.right = undefined
    }
}

class Tree {
    constructor(data) {
        // 临时存储所有节点，方便寻找父子节点
        let nodeList = []
            // 顶节点
        let root
        for (let i = 0, len = data.length; i < len; i++) {
            let node = new Node(data[i])
            nodeList.push(node)
            if (i > 0) {
                // 计算当前节点属于哪一层
                let n = Math.floor(Math.sqrt(i + 1))
                    // 记录当前层的起始点
                let q = Math.pow(2, n) - 1
                    // 记录上一层的起始点
                p = Math.pow(2, n - 1) - 1
                    // 找到当前节点的父节点
                let parent = nodeList[p + Math.floor((i - q) / 2)]
                    // 将当前节点和上一层的父节点做关联
                if (parent.left) {
                    parent.right = node
                } else {
                    parent.left = node
                }
            }
        }
        root = nodeList.shift()
            // 释放数组
        nodeList.length = 0
        return root
    }
}

export default Tree

export {
    Node
}

对称二叉树

给定一个二叉树，检查它是否是镜像对称的。

 // 例如，二叉树 [1,2,2,3,4,4,3] 是对称的。

    1
   / \
  2   2
 / \ / \
3  4 4  3
// 但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:

    1
   / \
  2   2
   \   \
   3    3

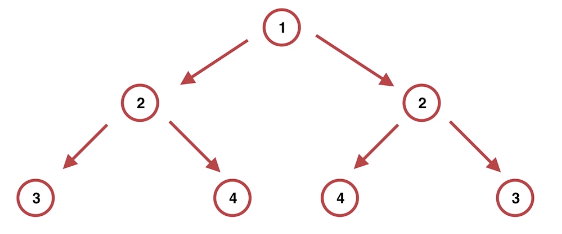
左定点的左节点等于右定点的右节点，以此类推

// 二叉树的节点
class Node {
    constructor(val) {
        this.val = val
        this.left = this.right = undefined
    }
}

class Tree {
    constructor(data) {
        // 临时存储所有节点，方便寻找父子节点
        let nodeList = []
            // 顶节点
        let root
        for (let i = 0, len = data.length; i < len; i++) {
            let node = new Node(data[i])
            nodeList.push(node)
            if (i > 0) {
                // 计算当前节点属于哪一层
                let n = Math.floor(Math.sqrt(i + 1))
                    // 记录当前层的起始点
                let q = Math.pow(2, n) - 1
                    // 记录上一层的起始点
                p = Math.pow(2, n - 1) - 1
                    // 找到当前节点的父节点
                let parent = nodeList[p + Math.floor((i - q) / 2)]
                    // 将当前节点和上一层的父节点做关联
                if (parent.left) {
                    parent.right = node
                } else {
                    parent.left = node
                }
            }
        }
        root = nodeList.shift()
            // 释放数组
        nodeList.length = 0
        return root
    }
    static isSymmetry(root) {
        if (!root) {
            return true
        }
        let walk = (left, right) => {
            if (!left && !right) {
                return true
            }
            if ((left && !right) || (!left && right) || (left.val !== right.val)) {
                return false
            }
            return walk(left.left, right.right) && walk(left.right, right.left)
        }
        return walk(root.left, root.right)
    }
}

export default Tree

export {
    Node
}

let root =new Tree([1,2,2,3,4,4,3])
console.log(Tree.isSymmetry(root))

验证二叉搜索树

给定一个二叉树，判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征：

• 节点的左子树只包含小于当前节点的数。
  节点的右子树只包含大于当前节点的数。
  所有左子树和右子树自身必须也是二叉搜索树。

// 示例 1:

输入:
    2
   / \
  1   3
输出: true

// 示例 2:

输入:
    5
   / \
  1   4
     / \
    3   6
输出: false
解释: 输入为: [5,1,4,null,null,3,6]。
     根节点的值为 5 ，但是其右子节点值为 4 。

所有的子树跳出来，看看是不是左边小右边大。如果所有都满足，那整个树都满足了

// 二叉树的节点
class Node {
    constructor(val) {
        this.val = val
        this.left = this.right = undefined
    }
}

class Tree {
    constructor(data) {
        let root = new Node(data.shift())
            // 遍历所有的数据，逐渐插入到当前这课搜索树中去
        data.forEach(item => {
            this.insert(root, item)
        })
        return root
    }
    insert(node, data) {
        if (node.val > data) {
            if (node.left === undefined) {
                node.left = new Node(data)
            } else {
                this.insert(node.left, data)
            }
        } else {
            if (node.right === undefined) {
                node.right = new Node(data)
            } else {
                this.insert(node.right, data)
            }
        }
    }
    static walk(root) {
        if (!root.left && !root.right) {
            return true
        } else if (((root.left && root.val < root.left.val) || (root.right && root.val > root.right.val))) {
            return false
        } else {
            return Tree.walk(root.left) && Tree.walk(root.right)
        }
    }
}
export default Tree
export {
    Node
}

二叉搜索树对于排序有很大参考。
做好了排序后，插入和删除非常好操作。