JS基础算法(数组篇) - sdk社区

1.公式运算（电话号码的组合）

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。
给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

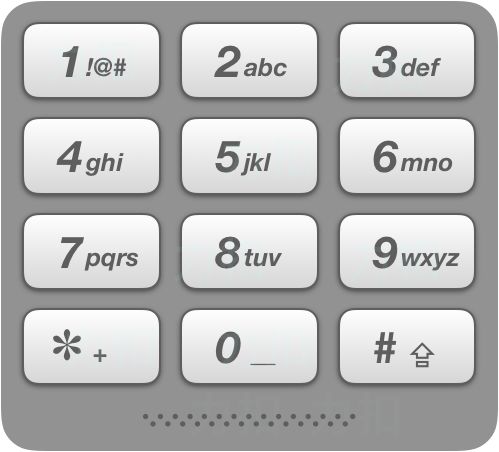
示例:

输入：“23” 输出：[“ad”, “ae”, “af”, “bd”, “be”, “bf”, “cd”, “ce”, “cf”]. 说明: 尽管上面的答案是按字典序排列的，但是你可以任意选择答案输出的顺序。

找出规律：只要前两项合并好,替代原来数组，再继续和后面合并
写出程序伪代码

export default (str) => {
  // 对输入做处理，如果小于1返回空（LeetCode测试用例）
  if (str.length < 1) return []
  // 建立电话号码键盘映射
  let map = ['', 1, 'abc', 'def', 'ghi', 'jkl', 'mno', 'pqrs', 'tuv', 'wxyz']
  // 如果只给了一个按键，直接把按键内容取出来并按单个字符分组就可以了（LeetCode测试用例）
  if (str.length < 2) return map[str].split('')
  // 把输入字符串按单字符分隔变成数组，234=>[2,3,4]
  let num = str.split('')
  // 保存键盘映射后的字母内容，如 23=>['abc','def']
  let code = []
  num.forEach(item => {
    if (map[item]) {
      code.push(map[item])
    }
  })
  let comb = (arr) => {
    // 临时变量用来保存前两个组合的结果
    let tmp = []
    // 最外层的循环是遍历第一个元素，里层的循环是遍历第二个元素
    for (let i = 0, il = arr[0].length; i < il; i++) {
      for (let j = 0, jl = arr[1].length; j < jl; j++) {
        tmp.push(`${arr[0][i]}${arr[1][j]}`)
      }
    }
    arr.splice(0, 2, tmp)
    if (arr.length > 1) {
      comb(arr)
    } else {
      return tmp
    }
    // 函数体应该返回第一个，最终只剩一个
    return arr[0]
  }
  return comb(code)
}

2.归类运算（卡牌分组）

给定一副牌，每张牌上都写着一个整数。

此时，你需要选定一个数字 X，使我们可以将整副牌按下述规则分成 1 组或更多组：
每组都有 X 张牌。
组内所有的牌上都写着相同的整数。
仅当你可选的 X >= 2 时返回 true。

示例 1：
输入：[1,2,3,4,4,3,2,1]
输出：true
解释：可行的分组是 [1,1]，[2,2]，[3,3]，[4,4]
示例 2：
输入：[1,1,1,2,2,2,3,3]
输出：false
解释：没有满足要求的分组。
示例 3：
输入：[1]
输出：false
解释：没有满足要求的分组。
示例 4：
输入：[1,1]
输出：true
解释：可行的分组是 [1,1]
示例 5：
输入：[1,1,2,2,2,2]
输出：true
解释：可行的分组是 [1,1]，[2,2]，[2,2]
提示：
1 <= deck.length <= 10000
0 <= deck[i] < 10000

看题目
答案都是排序的，所以需要先排序
相同数字过多需要拆分，是最大公约数即可

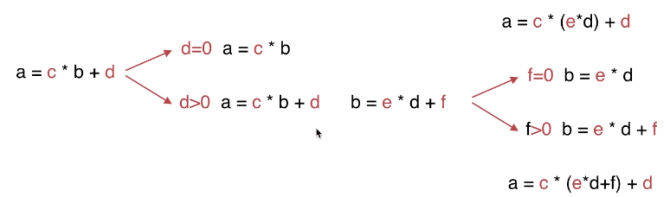
最大公约数：gcd(a,b) = gcd(b,a mod b)

export default (arr)=>{
  // 求最大公约数
  let gcd=(a,b)=>{
    if(b===0){
      return a
    }else{
      return gcd(b,a%b)
    }
  }
//   卡牌排序，排序的目的就是为了让相同的牌排在一起方便我们分组
  let str=arr.sort().join('')
  // 分组(单张或者多张)
  let group=str.match(/(\d)\1+|\d/g)
  while(group.length>1){
    let a=group.shift().length
    let b=group.shift().length
    let v=gcd(a,b)
    if(v===1){
      return false
    }else{
      // 结果放进去跟下一个比
      group.unshift('0'.repeat(v))
    }
  }
  return group.length?group[0].length>1:false
}

var hasGroupsSizeX = function(deck) {
        const map = {}
  let minLen = Number.MAX_SAFE_INTEGER
  let result

  // 卡牌按值分组
  deck.forEach(item => {
    if(!map[item]) {
      map[item] = []
    }
    map[item].push(item)
  })
  
  // 获取数量最少的卡牌数量
  Object.keys(map).forEach(item => {
    if(map[item].length < minLen) {
      minLen = map[item].length
    }
  })

  if(minLen === 1) {
    return false
  }

  // 从每组2张开始查看能否分组，能分组则返回true 
  for(let i = 2; i <= minLen; i++) {
    result = true
    Object.keys(map).forEach(item => {
      if(map[item].length % i !== 0) {
        result = false
      }
    })
    if(result) {
      return result
    }
  }
  
  return result;
};

var hasGroupsSizeX = function (deck) {
    // 统计数字个数
    const numMap = {}
    for (let i = 0; i < deck.length; i++) {
        if (!numMap[deck[i]]) {
            numMap[deck[i]] = 1
        } else {
            numMap[deck[i]]++
        }
    }
    const valuesArr = Object.values(numMap).sort((a, b) => a > b ? 1 : -1)
    // console.log('valuesArr', valuesArr)
    // 也就是说最大公约数得大于 1
    return !valuesArr.find(value => gcd(value, valuesArr[0]) === 1 || value < 2)

};

// 欧里几德算法，辗转相除法。
function gcd(a, b) {
    if (b == 0) {
        return a;
    }
    var r = parseInt(a % b);
    return gcd(b, r);
}

3.筛选运算（种花问题）

假设你有一个很长的花坛，一部分地块种植了花，另一部分却没有。可是，花卉不能种植在相邻的地块上，它们会争夺水源，两者都会死去。
给定一个花坛（表示为一个数组包含0和1，其中0表示没种植花，1表示种植了花），和一个数 n 。能否在不打破种植规则的情况下种入 n 朵花？能则返回True，不能则返回False。

示例 1:
输入: flowerbed = [1,0,0,0,1], n = 1
输出: True
示例 2:
输入: flowerbed = [1,0,0,0,1], n = 2
输出: False
注意:

数组内已种好的花不会违反种植规则。
输入的数组长度范围为 [1, 20000]。
n 是非负整数，且不会超过输入数组的大小。

技巧：把输入边长

// 场景一
[0,0,1,0,0,0,1,0,1,0,0,0,0,0,0,1,0,1]
// 场景二
[1,0,1,0,0,0,1,0,1,0,0,0,0,0,0,1,0,1]
[0,1,0,0,0,0,1,0,1,0,0,0,0,0,0,1,0,1]

问题：
边界问题（前后加个0可解决）
条件010 [0,0,1,0,0,0,1,0,1,0,0,0,0,0,0,1,0,1] +1 | |

export default (flowerbed,n)=>{
  let max = 0;
    flowerbed.push(0);
    flowerbed.unshift(0);
    let len=flowerbed.length;
    for (let i = 1; i < len-1; i++) {
        if (flowerbed[i-1] === 0 && flowerbed[i] === 0 && flowerbed[i+1] === 0) {
            flowerbed[i] = 1;
            max++;
        }
    }
    return max >= n
}

总结
学会问题抽象
学会数学建模思想
学会动态输入（多找输入，而不是通过该代码）

4.二进制运算（格雷编码）

parseInt(num,2)转换二进制为十进制 2. 注意两个连续的数值仅有一个位数的差异
格雷编码是一个二进制数字系统，在该系统中，两个连续的数值仅有一个位数的差异。
给定一个代表编码总位数的非负整数 n，打印其格雷编码序列。格雷编码序列必须以 0 开头。

示例 1:
输入: 2
输出: [0,1,3,2]
解释:
00 - 0
01 - 1
11 - 3
10 - 2
对于给定的 n，其格雷编码序列并不唯一。
例如，[0,2,3,1] 也是一个有效的格雷编码序列。
00 - 0
10 - 2
11 - 3
01 - 1
示例 2:
输入: 0
输出: [0]
解释: 我们定义格雷编码序列必须以 0 开头。
给定编码总位数为 n 的格雷编码序列，其长度为 2n。当 n = 0 时，长度为 20 = 1。
因此，当 n = 0 时，其格雷编码序列为 [0]。

export default (n)=>{
  // 递归函数，用来算输入为n的格雷编码序列
  let gray = function(n){
    if( n === 1){
      return ['0','1'];
    } else {
      let prev = gray(n-1);
      let res = [];
      let max = Math.pow(2,n)-1;
      for(let i =0;i<prev.length;i++){
        res[i] = `0${prev[i]}`;
        res[max - i] = `1${prev[i]}`;
      }
      return res;
    }
  }
  if(n === 0){
    return [0]
  }
  var res = gray(n);
  return res.map(item => {
    return parseInt(item,2)
  })
}

let grayCode = function(n){
    let arr=[];
      while(n--){
          let temp=[];
          if(arr.length===0){
              arr=[0,1];
              continue;
          }
          
          
          for(let i=0;i<arr.length;i++){
              for(let j=0;j<2;j++){
                  let num=parseInt(`${arr[i]}${j}`,2);
                  temp.push(num);
              }
          }
          arr=temp;
      }
    return arr;
}

发现规律，动态输入